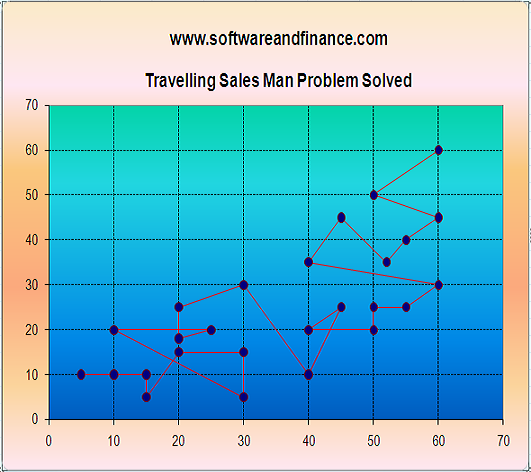
Viual C++ - Travelling Salesman Problem Solved
Travelling salesman problem can be solved easily if there are only 4 or 5 cities in our input.
But if there are more than 20 or 50 cities, the perfect solution would take couple of years to compute.
I have discussed here about the solution which is faster and obviously not the best solution using dynamic programming.
The idea that I have used here is to split the problem into small pieces and find the solution and then join them.
Source Code
#include "TSP.h"
#include <algorithm>
#include <math.h>
#include <string>
#include <vector>
#include <map>
#include <set>
using namespace std;
typedef struct _CITY_INFO
{
std::string cityname;
int x;
int y;
} CITY_INFO;
static CITY_INFO polypoints[] = {
{ "A", 5, 10 },
{ "B", 10, 20 },
{ "C", 15, 5 },
{ "D", 20, 15 },
{ "E", 25, 20 },
{ "F", 30, 30 },
{ "G", 20, 18 },
{ "H", 30, 5 },
{ "I", 30, 15 },
{ "J", 20, 25 },
{ "K", 6, 10 },
{ "L", 15, 10 },
{ "M", 40, 10 },
{ "N", 45, 25 },
{ "O", 40, 35 },
{ "P", 45, 45 },
{ "Q", 40, 20 },
{ "R", 52, 35 },
{ "S", 55, 40 },
{ "T", 50, 25 },
{ "U", 50, 20 },
{ "V", 55, 25 },
{ "W", 60, 30 },
{ "X", 50, 50 },
{ "Y", 60, 45 },
{ "Z", 60, 60 },
};
double CalculateDistance(CITY_INFO x, CITY_INFO y)
{
double result = sqrt( (double)(x.x - y.x)*(x.x - y.x) + (x.y - y.y)*(x.y - y.y));
return result;
}
int TSP_Helper(std::vector<CITY_INFO> &arr, double *dist, std::string &path, CITY_INFO &firstpoint, CITY_INFO &lastpoint)
{
int len = arr.size();
if(len > 5)
return -1; // Not Supported
double mindist = INT_MAX;
std::string str = "01234";
str = str.substr(0, len);
do
{
double distance = 0;
for(int i = 0; i < str.size() - 1; i++)
{
distance += CalculateDistance(arr[str[i]-'0'], arr[str[i+1] - '0']);
}
if( mindist > distance)
{
mindist = distance;
*dist = mindist;
path = "";
for(int i = 0; i < str.size(); i++)
{
path += arr[str[i]-'0'].cityname;
}
firstpoint = arr[str[0]-'0'];
lastpoint = arr[str[str.size() - 1]-'0'];
}
//std::cout << *dist << "\t" << str.c_str() << "\n";
} while(std::next_permutation(str.begin(), str.end()) != false);
}
bool SplitSet(const std::vector<CITY_INFO> &myset, std::vector<std::vector<CITY_INFO> > &mysplitset)
{
// Construct a grid
std::vector<CITY_INFO>::const_iterator it = myset.begin();
int minx = it->x;
int maxx = it->x;
int miny = it->y;
int maxy = it->y;
for(; it != myset.end(); ++it)
{
if(minx >= it->x)
minx = it->x;
if(maxx < it->x)
maxx = it->x;
if(miny >= it->y)
miny = it->y;
if(maxy < it->y)
maxy = it->y;
}
int width = maxx - minx;
int height = maxy - miny;
int midx = width / 2 + minx;
int midy = height / 2 + miny;
std::vector<CITY_INFO> s1, s2, s3, s4;
std::vector<CITY_INFO> *pset[] = { &s1, &s2, &s3, &s4 };
it = myset.begin();
for(; it != myset.end(); ++it)
{
// First Grid
if(it->x < midx && it->y < midy)
s1.push_back(*it);
// Second Grid
if(it->x >= midx && it->y < midy)
s2.push_back(*it);
// Third Grid
if(it->x < midx && it->y >= midy)
s3.push_back(*it);
// Fourth Grid
if(it->x >= midx && it->y >= midy)
s4.push_back(*it);
}
for(int i = 0; i < 4; i++)
{
if(pset[i]->size() <= 5)
{
if(pset[i]->size() > 0)
mysplitset.push_back(*pset[i]);
}
else
{
std::vector<std::vector<CITY_INFO> > tempset;
SplitSet(*pset[i], tempset);
for(std::vector<std::vector<CITY_INFO> >::iterator tit = tempset.begin();
tit != tempset.end(); ++tit)
{
if(tit->size() > 0)
mysplitset.push_back(*tit);
}
}
}
return true;
}
int TSP_Start(CITY_INFO *parr, int len, double *dist, std::string &finalpath)
{
int NumCities = len;
if(NumCities <= 5)
{
std::vector<CITY_INFO> myset;
for(int i = 0; i < len; i++)
{
myset.push_back(parr[i]);
}
CITY_INFO firstpoint, lastpoint;
TSP_Helper(myset, dist, finalpath, firstpoint, lastpoint);
}
else
{
std::vector<CITY_INFO> myset;
for(int i = 0; i < len; i++)
{
myset.push_back(parr[i]);
}
std::vector<std::vector<CITY_INFO> > mysplitset;
SplitSet(myset, mysplitset);
double distance = 0;
std::string result = "";
finalpath = "";
CITY_INFO firstpoint, lastpoint;
for(int i = 0; i < mysplitset.size(); i++)
{
std::vector<CITY_INFO> current = mysplitset[i];
if(i == 0)
{
double distSP = 0;
std::string path;
TSP_Helper(current, &distSP, path, firstpoint, lastpoint);
std::cout << "Path: "<< distSP << "\t" << path.c_str() << "\n";
distance = distSP;
finalpath = path;
}
else
{
double distSP = 0;
std::string path;
CITY_INFO fp, lp;
TSP_Helper(current, &distSP, path, fp, lp);
distance += distSP;
finalpath += path;
// Previous iteration last and current first point distance
std::vector<CITY_INFO> prev = mysplitset[i - 1];
// optimization required on this line!!!
// Distance between the last point and the closet point the current circuit would be taken here instead of first point
distance += CalculateDistance(lastpoint, fp);
lastpoint = lp;
firstpoint = fp;
std::cout << "Path: " << distance << "\t" << finalpath.c_str() << "\n";
*dist = distance;
}
}
}
return 0;
}
void main()
{
int NumCities = sizeof(polypoints) / sizeof(polypoints[0]);
double dist = 0;
std::string path;
TSP_Start(polypoints, 26, &dist, path);
std::cout << "\nPath: " << dist << "\t" << path.c_str() << "\n\n";
}
Output
Path: 15 AKLC
Path: 46.1803 AKLCDIH
Path: 71.1803 AKLCDIHB
Path: 109.746 AKLCDIHBEGJF
Path: 132.107 AKLCDIHBEGJFM
Path: 154.989 AKLCDIHBEGJFMNQ
Path: 182.06 AKLCDIHBEGJFMNQUTVW
Path: 213.856 AKLCDIHBEGJFMNQUTVWOP
Path: 238.964 AKLCDIHBEGJFMNQUTVWOPRSY
Path: 264.287 AKLCDIHBEGJFMNQUTVWOPRSYXZ
Path: 264.287 AKLCDIHBEGJFMNQUTVWOPRSYXZ
Press any key to continue . . .
|
|